Определённый интеграл от 0 до бесконечности

Определённый интеграл от 0 до бесконечности представляет собой математическую операцию, которая вычисляет площадь фигуры, ограниченной графиком функции и осью абсцисс в интервале от 0 до бесконечности. Этот тип интеграла широко применяется в различных областях науки и инженерии, таких как физика, экономика и статистика. Он позволяет решать задачи, связанные с накоплением или распределением величин, которые не имеют ограничений в виде верхней границы.

Что такое определённый интеграл?

Определённый интеграл обладает следующими свойствами:

• Является обратной операцией к дифференцированию
• Определяется двумя границами интегрирования (нижней и верхней)
• Может быть применен для нахождения площади, объема, центра тяжести и других величин

Формула определённого интеграла:

Определённый интеграл обозначается символом ∫ и записывается следующим образом:

∫[a, b] f(x) dx

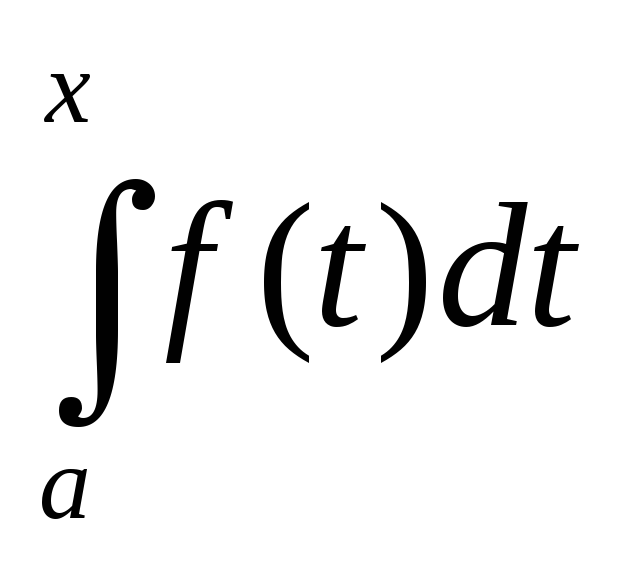
где:

• a — нижний предел интегрирования
• b — верхний предел интегрирования
• f(x) — функция, под которой вычисляется площадь
• dx — дифференциальная переменная

Определённый интеграл можно вычислить с помощью различных методов, таких как методы Римана, методы трапеций или методы средних.

Пример расчёта определённого интеграла:

Для наглядности рассмотрим пример вычисления определённого интеграла:

Дана функция y = x 2 + 1 и требуется вычислить определённый интеграл от 0 до 2.

Подставим значения границ интегрирования в формулу определённого интеграла:

∫[0, 2] (x 2 + 1) dx

Выполним интегрирование: возведём каждую переменную в степень и прибавим 1 к результату:

(x 3)/3 + x | [0, 2]

Подставим границы интегрирования:

((2 3)/3 + 2) — ((0 3)/3 + 0)

Выполним вычисления:

(8/3 + 2) — (0/3 + 0)

(8/3) + 2 = 14/3

Таким образом, определённый интеграл от функции y = x 2 + 1 на отрезке от 0 до 2 равен 14/3.

Примеры функций с определённым интегралом от 0 до бесконечности

1. Экспоненциальная функция

Функция вида f(x) = e (-x) имеет определённый интеграл от 0 до бесконечности и равен 1. Интеграл этой функции используется, например, при расчёте вероятности истинного события в статистике и теории вероятностей.

2. Обратная показательная функция

Функция вида f(x) = 1/x n (где n > 1) также имеет определённый интеграл от 0 до бесконечности. Интеграл этой функции используется, например, в физике для определения закона затухания электрического тока в цепи.

3. Гамма-функция

Гамма-функция, обозначаемая как Γ(x), является расширением факториала на комплексную плоскость. Она имеет определённый интеграл от 0 до бесконечности и может быть выражена через интеграл Эйлера-Пуассона. Гамма-функция имеет множество применений в математике, физике и статистике.

4. Синусоидальная функция

Функция вида f(x) = sin(x)/x является осциллирующей и имеет определённый интеграл от 0 до бесконечности. Эта функция встречается, например, в задачах связанных с колебаниями и волнами.

5. Нормальное распределение

Функция нормального распределения, также известная как функция Гаусса или экспоненциально-нормальная функция, имеет определённый интеграл от минус бесконечности до плюс бесконечности и равен 1. Нормальное распределение широко используется в статистике для анализа данных и вероятностных расчётов.

6. Логарифмическая функция

Функция вида f(x) = 1/(x * log(x)) (где log(x) — натуральный логарифм от x) также имеет определённый интеграл от 0 до бесконечности. Логарифмическая функция встречается, например, в задачах связанных с простыми числами и теорией чисел.

Это лишь несколько примеров функций, которые имеют определённый интеграл от 0 до бесконечности. Такие функции широко применяются в научных и инженерных расчетах, статистике, физике и других областях.

Как вычислить определённый интеграл от 0 до бесконечности?

1. Метод замены переменной

Один из способов вычисления определенного интеграла от 0 до бесконечности — это метод замены переменной. Для этого можно воспользоваться подстановкой, которая сводит задачу к вычислению интеграла от 0 до некоторого конечного числа. Затем проводится интегрирование, а полученный результат корректируется.

2. Метод интегрирования по частям

Метод интегрирования по частям также может быть полезен при вычислении определенного интеграла от 0 до бесконечности. Он основан на формуле интегрирования по частям, которая позволяет свести исходный интеграл к другому интегралу, который может быть проще вычислить. После нескольких итераций этого метода, интеграл будет уменьшаться, и его значение будет возможно вычислить.

3. Метод комплексного анализа

В случае, когда исходный интеграл является функцией, ограниченной на положительной полуоси, можно использовать методы комплексного анализа для его вычисления. Одним из таких методов является вычетный метод. Он основан на использовании вычетов интегрируемой функции в комплексной плоскости и формуле вычетов. С помощью этого метода можно свести задачу вычисления определенного интеграла от 0 до бесконечности к вычислению вычетов функции.

4. Использование таблиц интегралов

В некоторых случаях можно воспользоваться справочными таблицами интегралов, которые содержат значения интегралов для различных функций. Если исходная функция подходит под одну из формул в таблице, ее интеграл можно вычислить, заменив функцию в интеграле на ее значение из таблицы и вычислив полученный интеграл.

Пример вычисления определенного интеграла от 0 до бесконечности

Рассмотрим пример вычисления определенного интеграла от 0 до бесконечности следующего вида:

∫₀^∞ x² * e^-x dx

Можно воспользоваться методом интегрирования по частям:

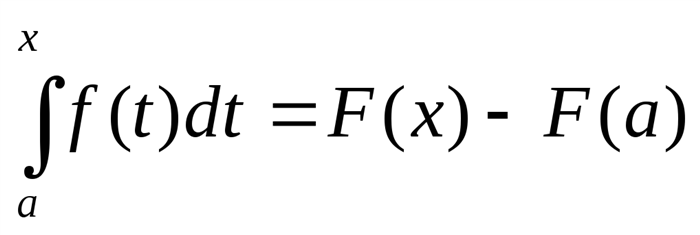
∫₀^∞ u dv = u v — ∫₀^∞ v du

Выберем:

u = x²

dv = e^-x dx

Тогда получим:

du = 2x dx

v = -e^-x

Подставим значения и проинтегрируем:

∫₀^∞ x² * e^-x dx = -x² * e^-x — ∫₀^∞ (-2x * -e^-x) dx

Упростим:

∫₀^∞ x² * e^-x dx = -x² * e^-x — 2 * ∫₀^∞ x * e^-x dx

Интеграл ∫₀^∞ x * e^-x dx также может быть решен методом интегрирования по частям или другими методами, как было описано ранее.

В результате, вычислив оба интеграла и произведя коррекцию, можно определить значение определенного интеграла от 0 до бесконечности для данного примера.

Графическое представление определённого интеграла от 0 до бесконечности

Определённый интеграл от 0 до бесконечности может быть графически представлен с использованием графика функции и площади под кривой.

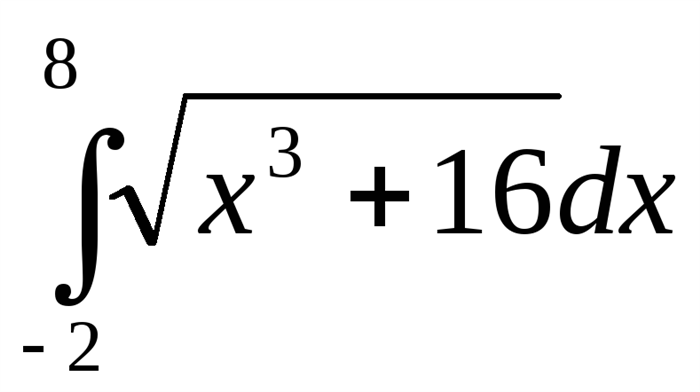
Построение графика функции

Перед тем, как рассматривать определённый интеграл, необходимо построить график функции, заданной в этом интеграле. Для этого следует:

1. Задать интервал значений для переменной, например, от 0 до бесконечности.
2. Вычислить значения функции для каждого значения переменной на заданном интервале.
3. Используя полученные значения, построить график функции на координатной плоскости.

Например, если задана функция f(x) = x 2, то график этой функции будет параболой, направленной вверх.

Площадь под кривой

Площадь под кривой на графике функции от 0 до бесконечности соответствует определённому интегралу от 0 до бесконечности этой функции.

Существует несколько способов оценки площади под кривой:

1. Метод прямоугольников: площадь под кривой оценивается прямоугольниками, наклоненными под углом к оси абсцисс.
2. Метод трапеций: площадь под кривой оценивается трапециями, соединяющими точки на графике функции.
3. Метод Симпсона: площадь под кривой оценивается параболами, которые аппроксимируют график функции.

Значение определённого интеграла

Значение определённого интеграла от 0 до бесконечности можно найти, вычислив площадь под кривой на графике функции. Чем точнее будет осуществлена оценка площади, тем ближе будет полученное значение интеграла к его истинному значению.

Метод	Преимущества	Недостатки
Метод прямоугольников	Прост в реализации	Не всегда точен
Метод трапеций	Более точен, чем метод прямоугольников	Требует больше вычислительных ресурсов
Метод Симпсона	Наиболее точен	Сложен в реализации

В итоге, графическое представление определённого интеграла от 0 до бесконечности позволяет наглядно увидеть зависимость площади под кривой от функции и понять, как изменяется значение интеграла при различных функциях и методах оценки площади.

Математические свойства определённого интеграла от 0 до бесконечности

Определённый интеграл от 0 до бесконечности обладает рядом важных математических свойств, которые позволяют упростить его вычисление и использование в различных задачах. Рассмотрим некоторые из них.

Линейность

Определённый интеграл от 0 до бесконечности обладает свойством линейности. Если функции f(x) и g(x) интегрируемы и константы a и b любые, то справедливо следующее:

∫₀^∞[a*f(x) + b*g(x)] dx = a*∫₀^∞f(x) dx + b*∫₀^∞g(x) dx

Интегрирование по частям

Для определённого интеграла от 0 до бесконечности существует формула интегрирования по частям:

∫₀^∞ u(x) v'(x) dx = [u(x)*v(x)]₀^∞ — ∫₀^∞ u'(x) v(x) dx

Изменение переменной

Определённый интеграл от 0 до бесконечности может быть упрощён путем замены переменной. Если x = g(t) является монотонной непрерывно дифференцируемой функцией и f(g(t)) и g'(t) интегрируемы, то справедлива следующая формула:

∫₀^∞ f(x) dx = ∫_a^b f(g(t)) g'(t) dt

Предел интеграла

Если функция f(x) ограничена и интегрируема на отрезке [0, c] для любого c > 0, то справедливо следующее утверждение:

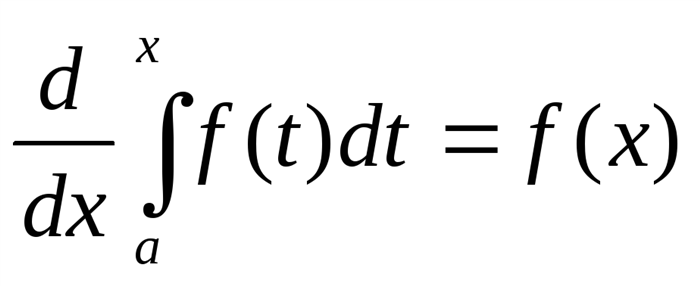
lim_c→∞ ∫₀^c f(x) dx = ∫₀^∞ f(x) dx

Интегрирование с параметром

Пусть функция f(x, a) интегрируема на каждом конечном отрезке [0, b], где b > 0. Если интеграл ∫₀^∞ f(x, a) dx сходится равномерно на [0, b] при a ∈ A, то для ∫₀^∞ f(x, a) dx справедливо следующее:

∫₀^∞ f(x, a) dx = ∫₀^∞ (∫_a^∞ f(x, a) dx) da

Таблица интегралов

Функция f(x)	Интеграл ∫0∞ f(x) dx
e-ax	1/a
1/(a2 + x2)	π/(2a)
sin(ax)	1/a
cos(ax)	1/a
e-x2	√π

Применение в задачах

Определённый интеграл от 0 до бесконечности широко применяется в различных математических и физических задачах. Например, он используется для вычисления площади под кривой, нахождения центра тяжести, расчёта вероятностей в статистике и теории вероятностей, решения дифференциальных уравнений и многих других задач. Знание его свойств и методов вычисления позволяет решать сложные задачи с помощью аналитических методов.

Существует ли определённый интеграл от 0 до бесконечности для всех функций?

Определённый интеграл от 0 до бесконечности существует не для всех функций, так как его сходимость зависит от свойств самой функции. Для определённого интеграла существуют определенные условия сходимости, которые функция должна удовлетворять.

1. Условия сходимости определённого интеграла

• Функция должна быть ограничена на промежутке от 0 до бесконечности;
• Функция должна быть интегрируема на каждом конечном промежутке от 0 до бесконечности;
• Интеграл от функции на каждом конечном промежутке должен сходиться.

2. Примеры функций с определённым интегралом от 0 до бесконечности

Некоторые функции, которые удовлетворяют условиям сходимости и имеют определённый интеграл от 0 до бесконечности:

1. f(x) = 1/x 2: интеграл от этой функции равен 1;
2. f(x) = e (-x): интеграл от этой функции также равен 1;
3. f(x) = 1/(x (1/2) + 1): интеграл от этой функции сходится и имеет конечное значение.

3. Примеры функций без определённого интеграла от 0 до бесконечности

Существуют функции, которые не удовлетворяют условиям сходимости и не имеют определённого интеграла от 0 до бесконечности:

1. f(x) = 1/x: интеграл от этой функции расходится и не имеет конечного значения;
2. f(x) = sin(x): интеграл от этой функции также расходится.

4. Значение определённого интеграла от 0 до бесконечности

Значение определённого интеграла от 0 до бесконечности может быть положительным, отрицательным или равным нулю в зависимости от функции. Сходимость или расходимость интеграла может быть использована для решения различных задач в математике и физике, позволяя вычислить площади, объёмы, вероятности и другие величины.

Функция	Значение определённого интеграла (от 0 до бесконечности)
f(x) = 1/x 2	1
f(x) = e (-x)	1
f(x) = 1/(x (1/2) + 1)	конечное значение
f(x) = 1/x	расходится
f(x) = sin(x)	расходится

Таким образом, не для всех функций существует определённый интеграл от 0 до бесконечности. Сходимость интеграла зависит от свойств функции и условий сходимости, которым она удовлетворяет.

Приложения определённого интеграла от 0 до бесконечности

Одно из основных применений определённого интеграла от 0 до бесконечности – в теории вероятностей. Он позволяет находить вероятность события, случайная величина которого является положительной и может принимать значения от 0 до бесконечности. Например, для распределения Пуассона или экспоненциального распределения можно использовать определённый интеграл для вычисления вероятности наступления события в заданный промежуток времени или при определённом количестве наблюдений.

Ещё одно применение определённого интеграла от 0 до бесконечности – в физике. Он позволяет вычислять массу, объем и центр тяжести тел, имеющих бесконечное распределение в пространстве. Также данный интеграл используется для моделирования и анализа процессов со взаимодействием, включая распределение энергии в спектре электромагнитных излучений, распределение зарядов в конденсаторах и электрических цепях, а также для расчёта полезной мощности в электрических сетях.

Помимо этого, определённый интеграл от 0 до бесконечности находит применение в экономике и финансах. Он позволяет оценить стоимость или доходность инвестиций, рассчитать вероятность получения прибыли или убытка при различных финансовых операциях, а также изучать зависимость доходности от времени.

В целом, определённый интеграл от 0 до бесконечности является мощным математическим инструментом, который играет важную роль в различных областях науки и инженерии. Используя его, можно решать разнообразные задачи, связанные с вероятностями, физикой, экономикой и многими другими дисциплинами.